used for classification

Motivation

• linear regression
• quantitative vs. qualitative(categorical) data quantitative data > regression quantitative Y qualitative data> classification qualitative Y class and regression can be used together

  Why not linear regression

• in case of variable Y with >2 categories: Coding categories as numbers (ordering and distance between categories) is arbitrary
• In case of variable Y with 2 categories: Coding with 0/1 would work
• Even with 2 categories there is an issue: Example: credit card default / not default 但是还是不好predict probability

  The Logistic Model

  main idea: predict probability P(Y=1| X=..)

  Logistic function

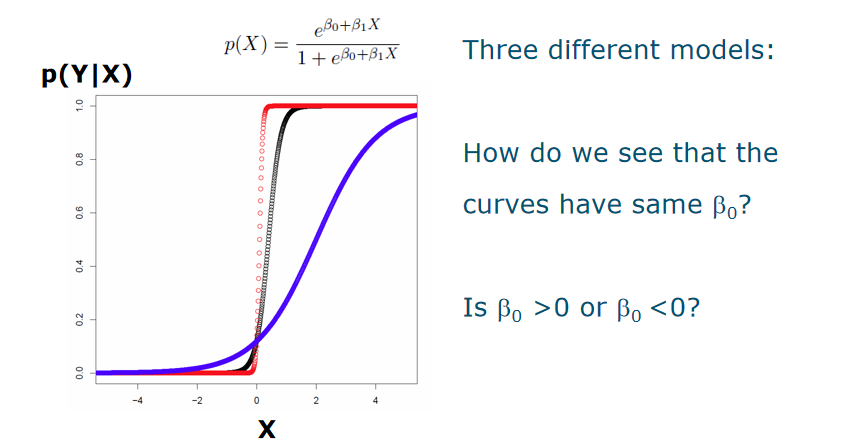
• S-shaped curve between 0 and 1: 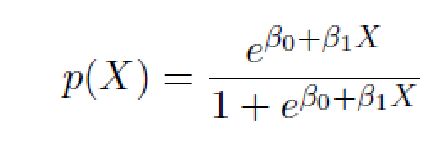这里Linear regression 范围会小于0，但是它的意义是概率
• How do we see that the curves have same B0? They cross the x= 0 at same point
• Is B0 >0 or B0 <0? if at the mentioned point the Y value is smaller than 0.5 , the B0<0 temperature of meidian low and high

  Odds

  The ratio of the probability of one event to that of an alternative event

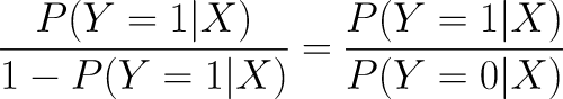
  Logistic function leads to logit that is linear in X

  Logit = log(Odds) 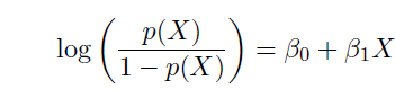B1 in linear regression: gives average change of Y associated with one-unit increase in X B1 in logistic regression: gives average change of log odds (logit) with one-unit increase in X

Exercise 9 (a)on average, what fraction of people with an odds of 0.37 of defaulting on their credit card payment will in fact default? (b)suppose that an individual has a 16% chance of defaulting on her credit card payment.What are the odds that she will default? 1 is default，越小越不default 0.37= x/1-x x= 0.16/1-0.16

Multiple Logistic Regression

how can we set decision boundary?this line will be 0.5?

Qualitative predictors

• 用dummies Number of dummy variables one lower than number of levels the variable has?？？？？？

  Parameter Estimation

  Maximum likelihood:

  定义：

• maximum likelihood: general approach to estimate model parameters用于估计参数的值，使得给定参数下数据观测到的概率（即似然函数）最大化
• Basic idea: the experimental observations are those that are likely to be observed
• Hence: find values for parameters such that the ==probability of the observed data is as large as possible==
• Likelihood: probability of the data given the parameters
• Define Likelihood L (for N datapoints) L=![[Pasted image 20240214112727.png]] The assumption of L : independent Optimal parameters given data: those that maximize L BUT，Instead of maximizing L, maximize log(L)

  推导：

  

  最后：

  当log(L)的负值最小（NLL negativate log-likelihood）的时候,或者Log-likelihood 的值最大的时候（就是越大越好，但是值是负的），逻辑函数通过优化算法（literative algorithm）之后，找到最好的b1,b2这些参数。 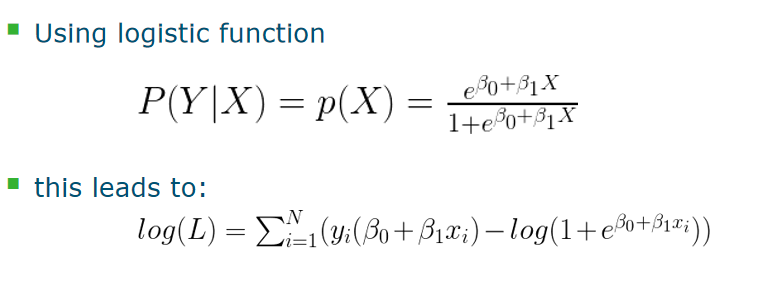这个式子的变形是：log (p /1−p) = β0 + β1X1 + β2X2 这里面的p的含义是 这个才我们要maximize的

  Some Consideration

  Interpretation of coefficient

  跟Linear regression 差不多，instead of t-statistic, we use Z-statistic

  Stability of parameter estimates

  problem:

  当模型参数的值发生变化时，模型的预测结果也会发生变化。如果模型参数的变化很大，那么模型的预测结果也可能会变得不稳定，即使输入数据没有变化。这种情况下，模型的参数估计是不稳定的。

  solution:

  regularization 通过在模型的损失函数中添加一个正则化项（regularization term），来限制模型参数的大小。这样可以降低模型参数的变化幅度，提高模型的稳定性。常用的正则化方法包括L1正则化（Lasso）和L2正则化（Ridge）等。

  Multiple predictors

  confounding

• confounding: a third variable (not the independent or dependent variable of interest) distorts the observed relationship between the variables of interest
• 为什么在引入income 变量之前student 的coefficient是正的，但是没引入这个变量之前student的coefficient是负的？ 因为：confounding

  Multinomial logistic regression

  ![[Pasted image 20240214222136.png]]

  Softmax regression

  Exercise ![[Pasted image 20240214222524.png]] （b）log (p /1−p) = β0 + β1X1 + β2X2

  Recap:

  Prediction of categorical Y given its features X is called…..classification Logistic regression: assume linear function for ……odds Parameter estimation: maximum likehood