Motivation

• prediction accuracy avoid overfitting 特别是p>n 的时候，就是变量大于样本量
• model interpreteability
• lower practical requirements:fewer measurements, less computation
• visualization, if selecting 2-3 features

  Introduction

  linear model, least squares minimization

  Solution

• feature subset selection: select
• feature extraction(PCA): map to
• shrinkage: adjust coefficients so that some features are used to a lesser extent (or not at all)
• regularization: reducing the model flexibility

  Feature subset selection

• Basic approach: select the best features
• Problem: the k best individual features are not necessarily the best set of k features(bc, the corelated )

  Best Subset Selection(Exhaustive)

• Search space 2^p -1 subsets
• Why not try all possible subsets then? 虽然尝试所有可能的子集是理论上的完美方法，但在实际情况下，由于搜索空间的巨大，这几乎是不可行的
• algorithm: 为了在这个庞大的搜索空间中找到最佳的子集，最佳子集选择方法通常使用贪婪算法。该算法从空集开始，然后在每一步中添加一个特征，从而构建一个特征子集。在每一步中，算法评估当前特征子集的性能，并选择对性能有最大贡献的特征添加到子集中。该过程一直持续到达到所需的特征数量k为止。
  • let M_0 denote the null model
  • for k =1,2….p>fit all models that use k predictors> M_k is the best of these(smallest RSS or largest R^2)> select a single best model from M_0….M_p based on CV error, C,AIC,BIC,adjusted R^2
• 缺点
  • computationally intensive
  • when 𝑝 is large, risk finding models that do well on training data but do not generalize well

    Stepwise Selection

    Forward Selection

• start with no predictors, iteratively add predictors until a stop criterion is reached
• Computational advantage is clear, but may miss optimal subset

Backward Selection

start with all predictors, iteratively removepredictors until a stop criterion is reached

• Computational advantage is clear, but may miss optimal subset
• Backward selection requires that 𝑛 > 𝑝 for fitting the full model, forward selection does not

  both

• both add/remove in each step the predictor that gives the greatest improvement/smallest deterioration
• search through only 1+p(p+1)/2
• are not guaranteed to find the best mode
• Hybrid approaches (“+l-r”):take l steps forward,then r steps back

  Choosing the optimal model

• Full model will always have the smallest RSS and the largest 𝑅2 – on the training datawould like to select model that performs best on test data
• 怎么选择
  • estimate test error indirectly, based on the training error: fast, but based on assumptions
  • estimate the test error directly,using a test set or cross-validation:more accurate, but slower

    Test set error estimates

    Mallow’s C_p AIC BIC Adjustes R^2

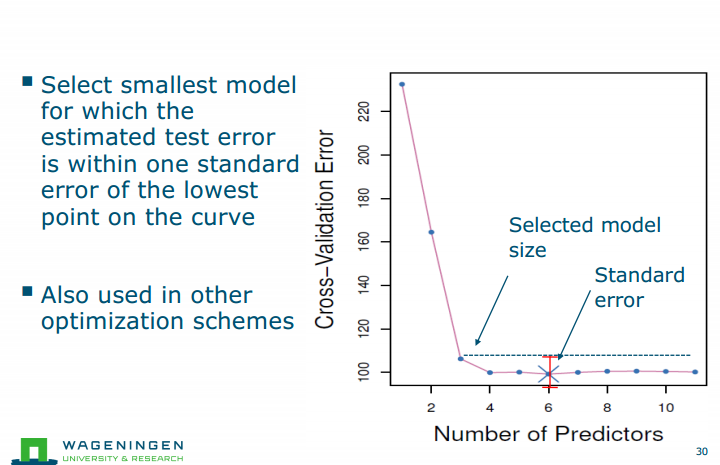
    One standard-error rule

    Exercise 1.We perform best subset, forward stepwise, and backward stepwise selection on a single data set. For each approach, we obtain p + 1 models, containing 0, 1, 2,…,p predictors. Explain your answers: (a) Which of the three models with k predictors has the smallest training RSS? (a) best subset//on training (b) Which of the three models with k predictors has the smallest test RSS? (b)it depends??? best subset (c) True or False: i. The predictors in the k-variable model identified by forward stepwise are a subset of the predictors in the (k+1)-variable model identified by forward stepwise selection. ii. The predictors in the k-variable model identified by backward stepwise are a subset of the predictors in the (k + 1)-variable model identified by backward stepwise selection. iii. The predictors in the k-variable model identified by backward stepwise are a subset of the predictors in the (k + 1)-variable model identified by forward stepwise selection. iv. The predictors in the k-variable model identified by forward stepwise are a subset of the predictors in the (k+1)-variable model identified by backward stepwise selection. v. The predictors in the k-variable model identified by best subset are a subset of the predictors in the (k + 1)-variable model identified by best subset selection (the best subset of k+1 does not necessarily contain the best subset of k variables) (c)True,False(True),False,False,True(False会变)

    Shrinkage

    increased bias, reduced variance

• adjust coefficients so that some features are used to a lesser extent (or not at all)
• Alternative to subset selection:shrink coefficients towards zero by constraining or regularizing

  Ridge Regression

  

• 第二项是shrinkage penalty: 当B接近0， 这个也很小
• Tuning parameter alamda control relative impact: 为0 就是普通的least squares, 无限大就all 𝛽=s will be zero (only intercept estimated)
• Selecting 𝜆 is critical: use cross-validation

  Scaling

• Standard least squares is scale equivariant: multiplying 𝑋𝑗 by a constant 𝑐 means 𝛽𝑗 scales by a factor of 1/𝑐: 𝑋𝑗 𝛽𝑗 will remain the same.
• Ridge regression is scale-sensitive, due to the penalty
• Solution: normalize predictors first

  Bias-variance

• Ridge regression reduces flexibility: decreases variance at the cost of increased bias
• 𝜆 controls flexibility of predictor 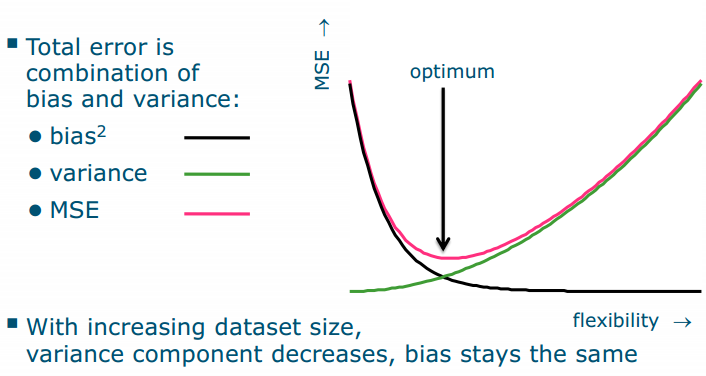With increasing dataset size,variance component decreases, bias stays the same flexibility variance 是关注敏感度，bias是关注灵活度，如果数据变多，variance就会更不敏感，所以就下降。

  The Lasso

• Disadvantage of ridge regression: all 𝑝 predictors are still used in the final mode ![[cd6f3e58f5d5e26790efb184abcdddd.png]]
• Also shrinks coefficients towards zero, but 𝑙1 penalty forces some to be exactly zero
• actually performs variable subset selection
• yields sparse models, with just a small set of variables 稀疏模型

  Lasso vs. ridge

  Why does lasso give coefficients of zero? ![[3e6d927a87d19d9b3a06d8b91a88ae5.png]] 2.For parts (a) through (c), indicate which of i. through iv. is correct. Justify your answer. (a) The lasso, relative to least squares, is: i. More flexible and hence will give improved prediction accuracy when its increase in bias is less than its decrease in variance. ii. More flexible and hence will give improved prediction accuracy when its increase in variance is less than its decrease in bias. iii. Less flexible and hence will give improved prediction accuracy when its increase in bias is less than its decrease in variance. iv. Less flexible and hence will give improved prediction accuracy when its increase in variance is less than its decrease in bias. (b) Repeat (a) for ridge regression relative to least squares. (c) Repeat (a) for non-linear methods relative to least squares. 2.i, i, iv»> iii,iii, ii

4.Suppose we estimate the regression coefficients in a linear regression model by minimizing for a particular value of λ. For parts (a) through (e), indicate which of i. through v. is correct. Justify your answer. i. Increase initially, and then eventually start decreasing in an inverted U shape. ii. Decrease initially, and then eventually start increasing in a U shape. iii. Steadily increase. iv. Steadily decrease. v. Remain constant. (a) As we increase λ from 0, the training RSS will:iii (b) Repeat (a) for test RSS. ii (c) Repeat (a) for variance. iv (d) Repeat (a) for (squared) bias. iii (e) Repeat (a) for the irreducible error. v 4, iv, ii, ii, iv, v.»> iii,ii, iv ,iii , v (就是lamda变化， 模型的复杂度也会变化，然后再想这个东西怎么变化)

High-dimensional spaces

Modern sensors yield many variables - often 𝑝 ≫ n Most (statistical) approaches were developed for problems with few variables

Overfitting

• Least squares does not work when 𝑝 > 𝑛 : too flexible
• Even when 𝑝 < 𝑛, danger of overfitting

  Curse of dimensionality

  就是本来越多的features 应该给我们更多的信息，但是 the number of parameters to estimate increases with the number of measurements 为了估计这些Parameters就要更多的samples. Consequence: given a certain number of samples there is an optimal number of features to use.

  Model performance vs. flexibility

  largest risk in modelling is overfitting就是因为对训练集拟合的太好了，导致不能很好的泛化别的数据集了 Model overfits when it performs (much) better on training data than on test data