Decision Trees

We categorize data through chain of simple decisions. a binary tree, which is a graph data structure in which each node has at most two children

Terminology

input features: data to be classified root node: starts the decision process decision nodes: Each decision node (split node) implements a test function with discrete outcomes The test function of each decision node splits the input space into regions leaf nodes: A leaf node indicates the end of a sequence of decisions A single (output) class is associated to each leaf node

Algorithm to make predictions

Increasing node purity

every decision should increase the node purity

Quantifying Node Purity

Measuring Node Purity

• Low Entropy: more pure;Higher Entropy: less pure»H(p) how flat
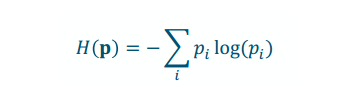
• Gini Index: higher gini index ,less pure 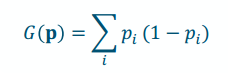0.25* 0.75 4 times 0.45* 0.55 2 times + 0.05 * 0.95 2 times

  Regression Trees

  leaf nodes return the average sample variance as node purity,high variance before splitting, low variacne after splitting

  Classification versus Regression Trees

  How to find the thresholde t?

  Try different thresholds optimum as best recordede threshold

  Binary Splitting

  we test as many thresholds as we have points ![[ab2533bf07de0f47d6c10fc874cc20f.png]]

  Growing a Decision tree with Recursive Binary Splitting:

• perform binary splitting
• recursively for each decision node
• to maximize node purity
• We end uo with one sample per node = a 1-NN regressor/classifier

  Overfitting of DTs

• Tree fits training data perfectly (zero variance)
• Tree extremely large, and uninterpretable

  Regularization of DTs

  Restricting Depth

• Tree fits training data perfectly (zero variance)
• Tree extremely large, and uninterpretable

  Tree Pruning

  Slow Grows（限制生长，greedy）

  Strategy: Grow first the tree slowly with additional checks during growing • Simple checks: maximum depth,max number of leaf nodes. • Add decision node only if increase in node purity is above a certain threshold

  Fast Cutters(先长再切, non-greedy)

  Strategy: Grow the full tree and then remove not important nodes later. • Cost complexity pruning: we identify the weakest link in the tree to remove

  Cost Complexity Pruning

• Remove leafs to reduce the complexity, while maintaining a low training error, i.e., cost. The hyperparameter 𝛼 balances both objectives.

• Clamada(T) = C(T) + lamada

  T

  就是cost(training error)+complexity(number leafs)

• higher alpha: produces shallower tree with less nodes

  如何利用 cost complexity pruning来构建树

  ![[638c2052311e5c539c5d454e45e1a73.png]]

  Advantages and Disadvantages of Trees

  Advantages: ● Inexpensive to construct ● Extremely fast at classifying unknown records ● Easy to interpret for small-sized trees ● Robust to noise (especially when methods to avoid overfitting are employed) ● Can easily handle redundant or irrelevant attributes (unless the attributes are interacting) Disadvantages: ● Space of possible decision trees is exponentially large. Greedy approaches are often unable to find the best tree. ● Does not take into account interactions between attributes ● Each decision boundary involves only a single attribute ● too deep ,more sensitive to noise

  Bagging, Forest,Boosting

• Bagging是在干啥： we split the feature space into regions The modes(i.e., centers) of the data distributions are well assigned to the classes. But the uncertain overlapping region is a mess

• low bias each tree fiting vey well
• high variance > difference between different trees higher

  Bias - Variance Trade-off: Finding a balance between fitting and overfitting

  for tree-like classifiiers

  Strategy 1: Reduce DT complexity

• Greedy (restrict DT complexity)
• Non-greedy (post-hoc pruning of the decision tree)

  Stragegy 2 Ensemble multiple Decision Trees together集成多个决策树：森林！！

  Step 1 Bagging

• split different data subset: randomly sampled subsets (bootstrap)
• ensemble prediction: majority voting for classification output averaging for regression
• effect: Decision boundaries become blurry: more realistic boundary

  Out-of-Bag Error Estimation

  Process:

  1. Fit decision tree DT_i on 𝒟_i ,
  2. Test its performance on the out-of-bag set 𝒟_oob
  3. Repeat for each tree in the bag Idea: - This OOB error approximates the test error.
• Similar idea to cross-validation, but for every DT separately

  Re-gaining Interpretability

• Bagging trees improves accuracy over a single tree through increasing diversity in the decisions 意思就是随机性增加了，所以增加了精度
• But we loose interpretability: Each tree has different decision rules Interpreting many decision rules in parallel is difficult
• Strategy: Measure the increase in node purity across trees
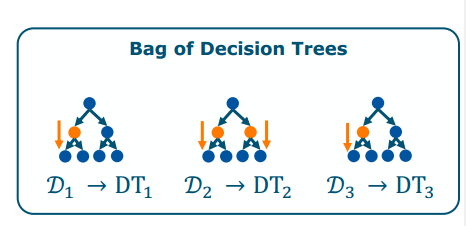• 就是看每个感兴趣点（橘色点）的node purity，然后求平均

  if bagging trees are still highly correlated with each other

  

Step 2 Random forest

• Idea: increase diversity by removing features from individual trees (removing the root node , to increase diversity)
• Implementation:we take a random sample of predictors for each tree (usually 根号下 𝐹)(for instance, 4 features out of 15)
• for each decision tree : 随机trained with a dataset subset和 subset of features
• Bags and Random Forest:
  • each tree is trained on a different “bootstrapped” set of train data
  • trees are trained separately from each other in parallel
• Random Forests: additionally each tree is trained with a different subset of features

  Boosting

  Random Forest versus Boosting Philosophy

• Random Forest: accuracy through classifier diversity all trees grown in parallel
• Boosting: many small “weak” classifiers trees grown sequentially

  Principles

• Train one classifier after another
• Reweight the data so that wrongly classified data is more important (grow it one by one, there is order of importance)

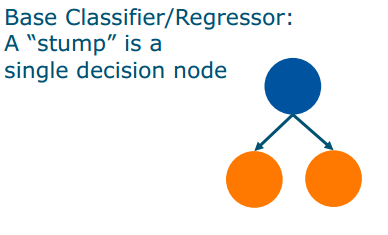
  AdaBoost

  Three Core Ideas:

• Combines many “weak learners”
• some stumps are weighted higher than others
• each stump takes the previous stumps into account