Separating Hyperplanes

• when you want to find a decision boundary, avoid estimating densities
• linear decision boundry,就是设置这个式子为0，就是它的decision boundry hyperplanes separate feature space into regions
• for new X, 可以带入最后一个式子，然后看y=1,还是y=-1来分类 exercise1. This problem involves hyperplanes in two dimensions. (a) Sketch the hyperplane 1 + 3X1 − X2 = 0. Indicate the set of points for which 1 + 3X1 − X2 > 0, as well as the set of points for which 1 + 3X1 − X2 < 0. (b) On the same plot, sketch the hyperplane −2 + X1 + 2X2 = 0. Indicate the set of points for which −2 + X1 + 2X2 > 0, as well as the set of points for which −2 + X1 + 2X2 < 0.

  Maximum margin classifiers

  （怎么找一个最佳的hyperplane）

• generalization link to regularization
• for generalization, the decision boundary should lie between the class boundaries
• Maximize perpendicular distance(最大化垂直距离) between the decision boundary and the ==nearest observations==: the margin M the decision boundary then only depends on a few points on the margin, the support vectors:if you remove one from other ob, nothing changes
• 所以， leave one out will fail

  Construction

  maximize the margin（尝试最大边际化）, under the constraint that training observations are classified correctly

  Limitation

  ● separable classes ● linear separability ● two classes

  Problems

• Maximum margin classifier is prone to ==overfitting==: very sensitive to training set
• When classes ==overlap==, separating hyperplane does not exist
• We need to make a trade-off between errors on the training set and predicted performance on the test set (generalization)

  Solution: The soft margin

  为了解决上面的问题

• Solution: ==allow (some, small) errors on the training set,==introducing slack （松弛）variables ∊i ≥ 0»>Add slack variables to maximum margin classifier, but limit total slack to C: the trade-off parameter
• 变化：M» M(1-e)，然后引入一个C，误差平方和<=C
• C influence solution: There is no a prori best choice for C

  The multi-class case

• one-versus-one
• one- versus-all exercise

  Optimization(optional)

  从最大化M(margin)到最小化一个系数w和常数b的平方和 但是为了解决is a (large) quadratic programming (QP) problem 又引入了lagrange multipliers alphai

  The nonlinear case

  Ideal: classes may become linearly separable if higher order terms are added(cf. nonlinear regression) ![[22e573c5252d8db1948d586ddaa54dd.png]]

  Questions

• feature是要平方还是开方，等等，我不知道
• efficiently train the SVC,就是p= 10 ,如果要3次，就会有286种组合方式了

  The Kernel Trick

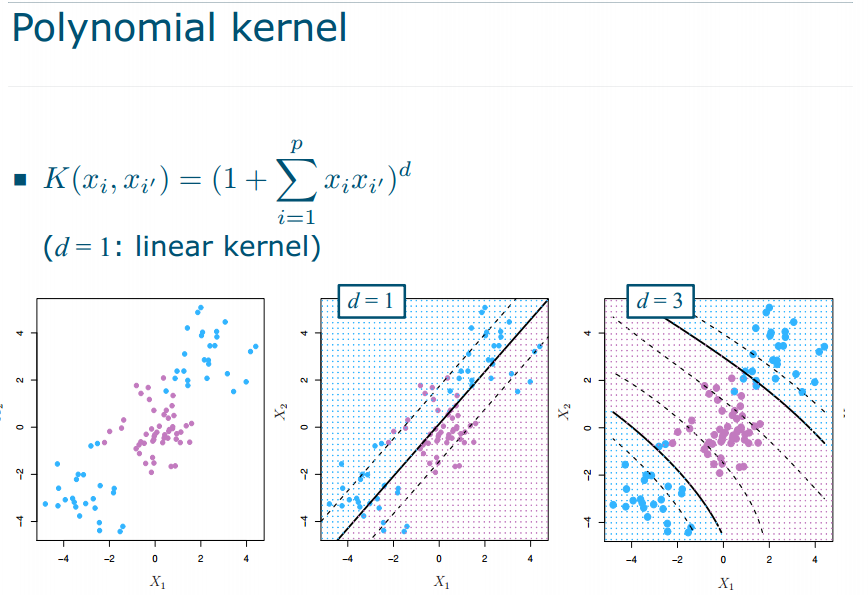
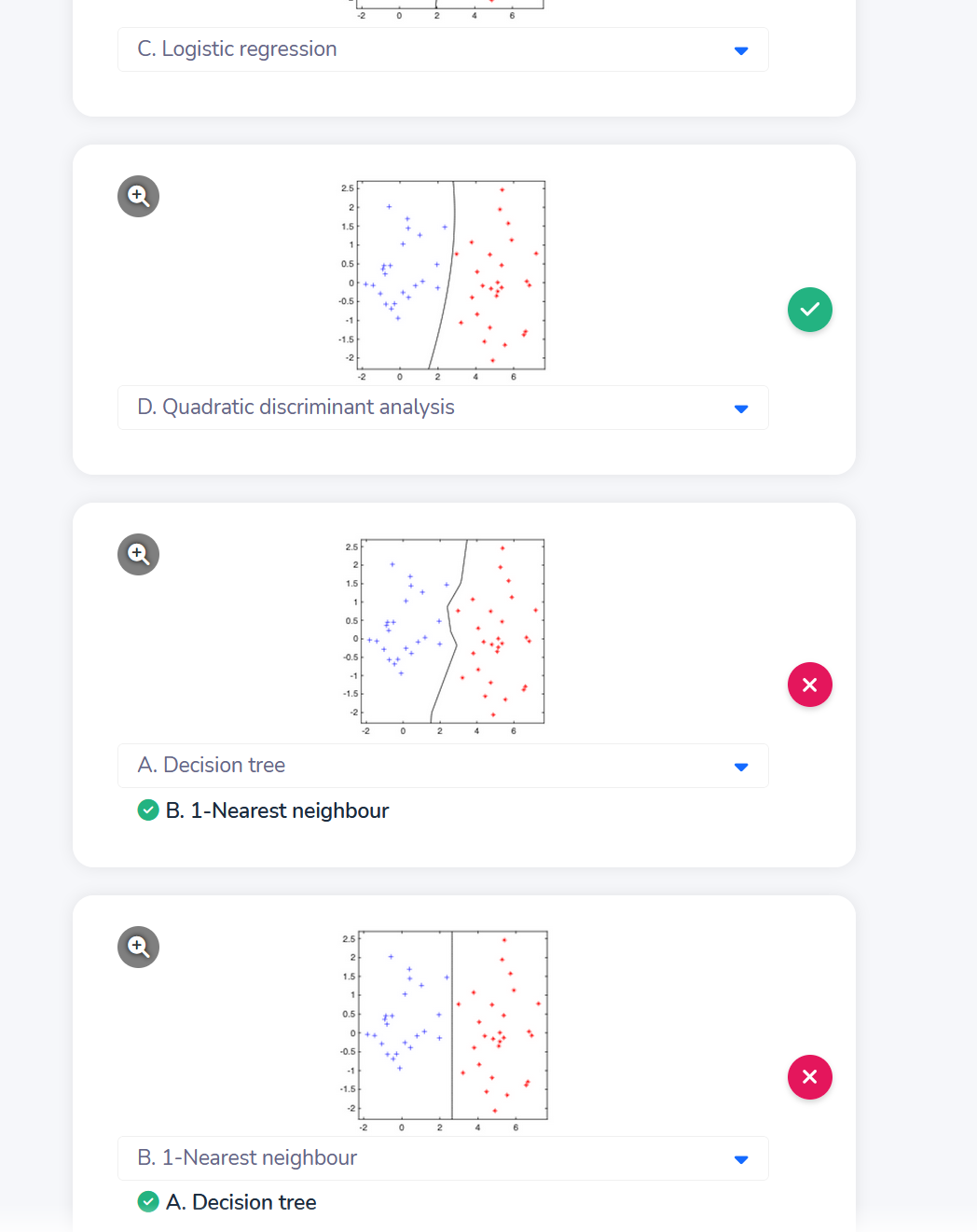
  训练阶段，我们需要计算所有训练样本之间的内积，如 xi 和 xi’ 之间的内积。训练完成后，当我们需要对新的样本进行分类时，我们只需要计算支持向量 (support vectors) 与新样本之间的内积。 引入一个用于泛化的核函数Think of kernel functions as similarities: large when the inputs are very alike, small when they are not 到这一步了，才有两种方法可以选择K（x_i, x）

• Polynomial kernel
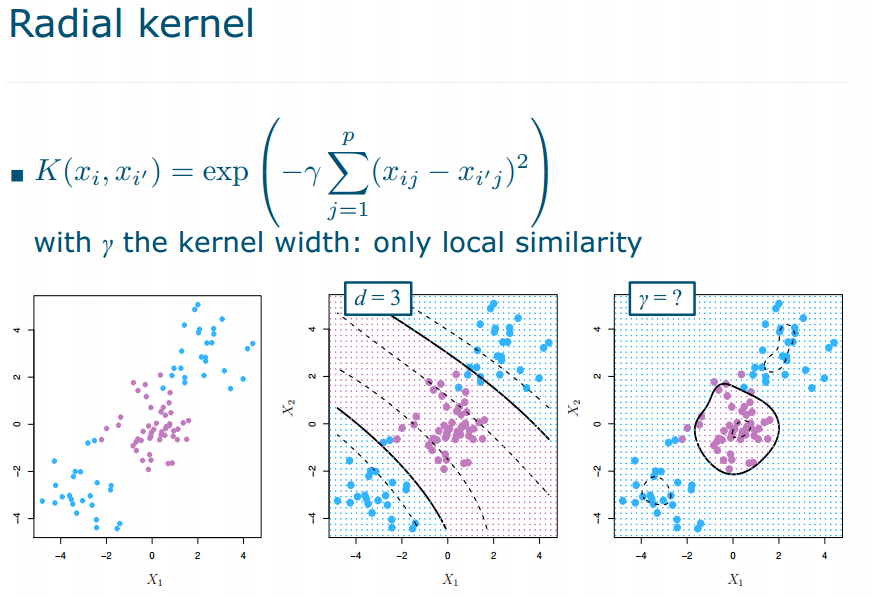
• Radial kernel

  The support vector machine

  Choosing Kernels

  What kernel functions should we use? type: prior knowledge of problem, trial-and-error parameters: cross-validation, like for C exercise

  More Kernels

  A large number of kernels have been proposed,not limited to numerical/vector data! ● Vector kernels ● Set kernels ● String kernels ● Empirical kernel map ● Kernel kernels ● Kernel combination ● Kernels on graphs ● Kernels in graphs ● Kernels on probabilistic models

  Recap

• Separating hyperplane: any plane that separates classes
• The support vector machine has evolved from fundamental work by Vapnik: separable, linear problems: maximum margin classifier non-separable, linear problems - add slack variables:support vector classifier non-separable, non-linear problems - use kernel trick:support vector machine
• Training involves quadratic programming (optimization)

• The final classifier only depends on the support vectors

• SVMs are widely used and work well in many cases,but care needs to be taken in selecting C, the kernel type and its parameters (using cross-validation)
• The kernel trick: replace inner products by more general kernel functions can be applied in many other algorithms
• Many kernels have been proposed for non-vector data, i.e. sets, strings, graphs etc.: very useful in bioinformatics, vision, document analysis etc.
• SVMs are linked to logistic regression (section 9.5, not discussed here)

  Support Vector

  Support Classifiers