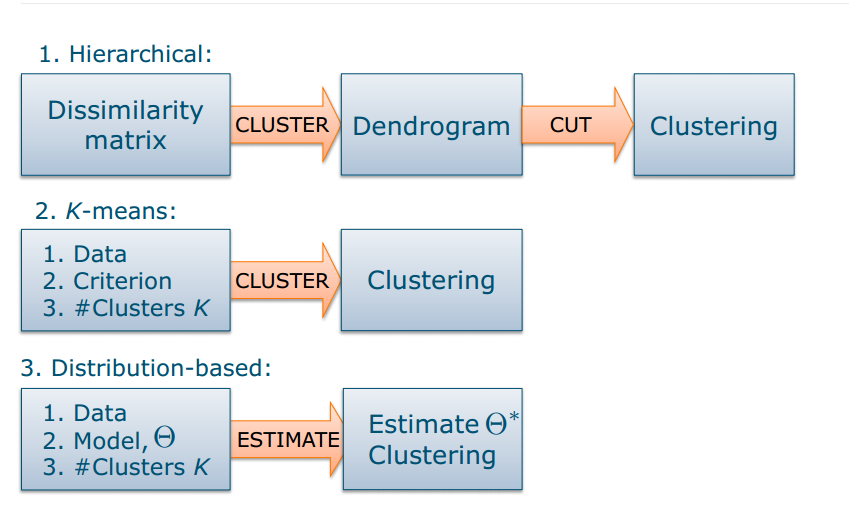
Clustering methods–Hierarchical

• dissimilarity matrix(cluster)dengrogram(cut)clustering
• bottom-up or agglomerative(as opposed to top-down or divisive)
• Disadavantages: once clustered, objects stay clustered, hard clustering: objects are assigned to a single cluster

  Clustering methods–K-means

  Data, Criterion, Clusters K(cluster)Clustering For every selected number of clusters K, choose optimal clustering What is optimal?

  K-means definitions

• 都是并集，clusters do not overlap
• Optimal clustering:squared distances between all pairs in each cluster or, equivalently, squared distances to cluster means, are minimal
• 
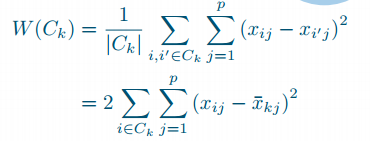
• problem: need known W(C_k), but there are possibilities (!)
• iterative optimization

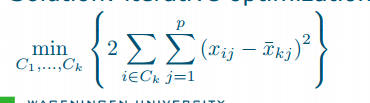
  K-means algorithm

  就是k means是表示xi只属于一个簇，所以我定下有k个簇，我随机把数据点放到这些簇里，然后求每个簇的平均值（和方差），找离这个簇最近的点，迭代一遍所有点，让分类的结果最后不变

  1. Choose number of clusters K and randomly assign each sample to a cluster
  2. Iterate until nothing changes: (a) for each cluster, calculate the centroid (mean) (b) re-assign each sample to the cluster whose mean is closest (in the Euclidean sense)
• Guaranteed to only decrease the criterion (why?):这个过程可以保证每次迭代都至少不会增加目标函数的值。 exercise 3

  Choice of K

  Rule of thumb: look for “drop” in criterion

  K-means problems

  Clusters can lose all samples

  Why

  1. 初始质心选择不当：如果初始质心选取不当，有些质心可能会被分配到一个不包含任何样本的区域。这会导致该簇失去所有的样本。
  2. 非凸形状的簇：如果数据集包含非凸形状的簇，例如环状或月牙形状的簇，K-means 算法可能会将其分割成多个较小的簇，导致某个簇失去所有的样本。
  3. 数据量不均衡：如果某个簇中的样本数量太少，而其他簇中的样本数量较多，则某个簇可能会失去所有的样本，因为K-means 算法的更新过程是基于样本的平均值。

     Solutions

  4. remove cluster and continue with K – 1 means
  5. alternatively, split largest cluster into two or add a random mean to continue with K means

     Clustering result depends on initialization –Algorithm can get stuck in local minima

     Solution:

  6. start from (many) different random initialisations
  7. keep the best clustering(lowest sumW(C_k))

     Limitations

     K-means model not necessarily optimal Equal cluster models not necessarily optimal Hard clustering not necessarily optimal exercise

     The K-means model

     What cluster model actually underlies K-means? ● spherical, uniform ● implicit in criterion Choosing an explicit model can help to: ● understand the result ● quantify the model fit ● try alternative models ● make assumptions explicit

     Mixture Models

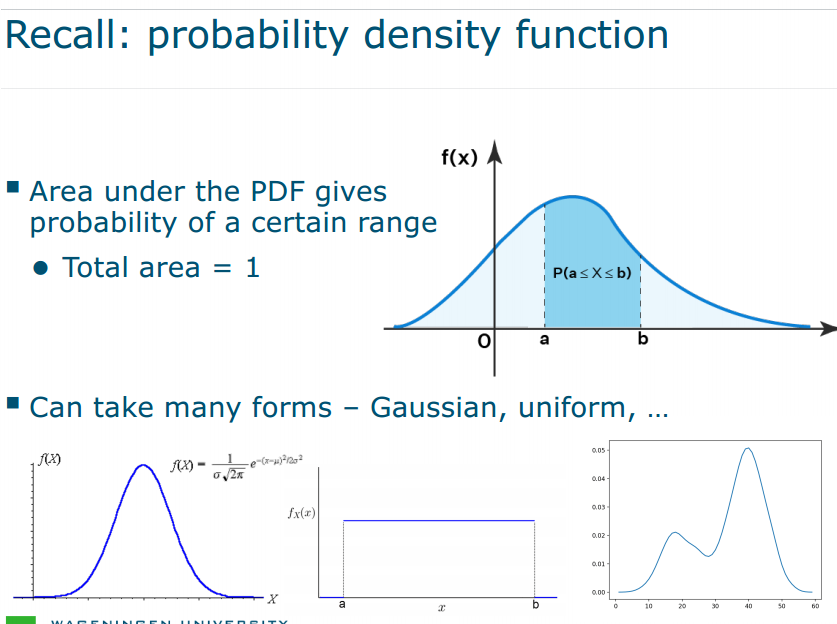
     Model the probability distribution of the data

• gives model for overall data distribution
• "soft" clustering: captures uncertainty in assignments
• parameters can be found using maximum likelihood

  Distribution-based clustering

• Each cluster is described by a probability density function
• Total dataset described by a mixture of density functions
• Clustering means maximizing the mixture fit,
• cluster assignment is based on posterior probabilities 就是我要知道x这个点属于每个簇的概率，把x分配给概率最高的簇，但是给定k簇的情况下求x(就是已经知道一个点属于k，求这个点是x点的概率)更好求（高斯的分布的密度函数求,就是用平均值和平方和求），所以先求这个。

  Fitting mixture models

  对于混合高斯模型，我们有以下步骤：

  1. 初始化参数：我们首先随机初始化每个高斯分布的均值、方差和权重。
  2. 计算每个样本属于每个高斯分布的概率：对于每个样本xi​，我们计算它属于每个高斯分布 k 的概率 P(xi​∣k)。（Note that mixture models also work for other component densities!）
  3. 更新参数：对于每个高斯分布 k，我们根据每个样本属于该分布的概率来更新均值、方差和权重。这个更新过程使用最大似然估计的方法。(说白了就是选最大的概率)
  4. 重复步骤2和3：我们重复步骤2和3，直到参数不再改变或达到最大迭代次数。
  5. 输出参数：最终，我们输出参数的估计值，这些参数可以用来描述数据的分布情况。

     Mixture of Gaussians

     

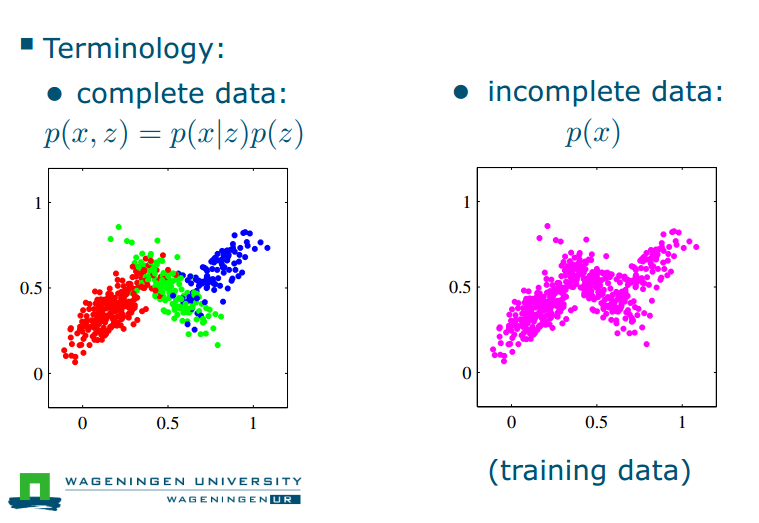
     Latent variable

     Problem:

     need to simultaneously estimate two interdependent things… no closed form solution! cluster membership of each object

     solutions

     

     The EM algorithm

     Expectation-Maximization algorithm:

• general class of algorithms for this type of problem
• repeatedly: recalculate cluster membership of each sample (E) recalculate density parameters of each cluster (M) EM算法是一种求解含有隐变量的概率模型的参数估计方法。它的基本思想是：假设观测数据的生成过程包含两个步骤，即隐变量的生成和观测数据的生成。在E步，算法利用当前参数估计隐变量的后验概率，即估计隐变量的分布；在M步，算法利用E步的结果估计模型参数。通过反复迭代E步和M步，最终达到收敛。EM算法的目标是最大化似然函数，使得观测数据的生成概率最大，从而得到最优的参数估计。

  The EM algorithm for MoGs

  EM 就是隐变量的概率我知道（但是会随着高斯分布的均值和协方差变化而变化），求浅变量的概率就是求responsibility，（把这个代入这个高斯求浅变量的式子里面就是Estep），用最大似然法找到最大的（把式子求导找极值）就是Mstep EM 就是隐变量的概率我知道（但是会随着高斯分布的均值和协方差变化而变化），求浅变量的概率就是求responsibility，用最大似然法找到最大的（在M步中，我们通过最大化似然函数来更新模型参数估计，例如我们可以通过对似然函数求导，令导数为0，找到似然函数的最大值点，这个过程通常称为最大似然估计（MLE））

K-means is a special case of a mixture-of-Gaussians 如果每一个点，到每一个簇的概率都是相等的，就是Kmeans,但是如果不是相等的，就是mog。 在K-means算法中，每个簇的协方差矩阵是对角矩阵，并且每个元素相等。

Limitations

• Disadvantages (similar to K-means): ● depends on initial conditions, can get stuck in local minima: same solution局部最优 ● convergence can be slow收敛很慢 ● problems with covariance estimates: if too few samples are members of a cluster, there will not be enough data to base estimate on 样本太少
• Advantages: ● simple to implement简单 ● can use prior knowledge of cluster distribution可以用先验概率