Sampling Methods and Model Selection

8 Cross-Validation

1. 生成数据集
2. 设置随机种子，然后计算使用最小二乘拟合以下四个模型（增加次数的一次到四次的多项式）所产生的 LOOCV 误差
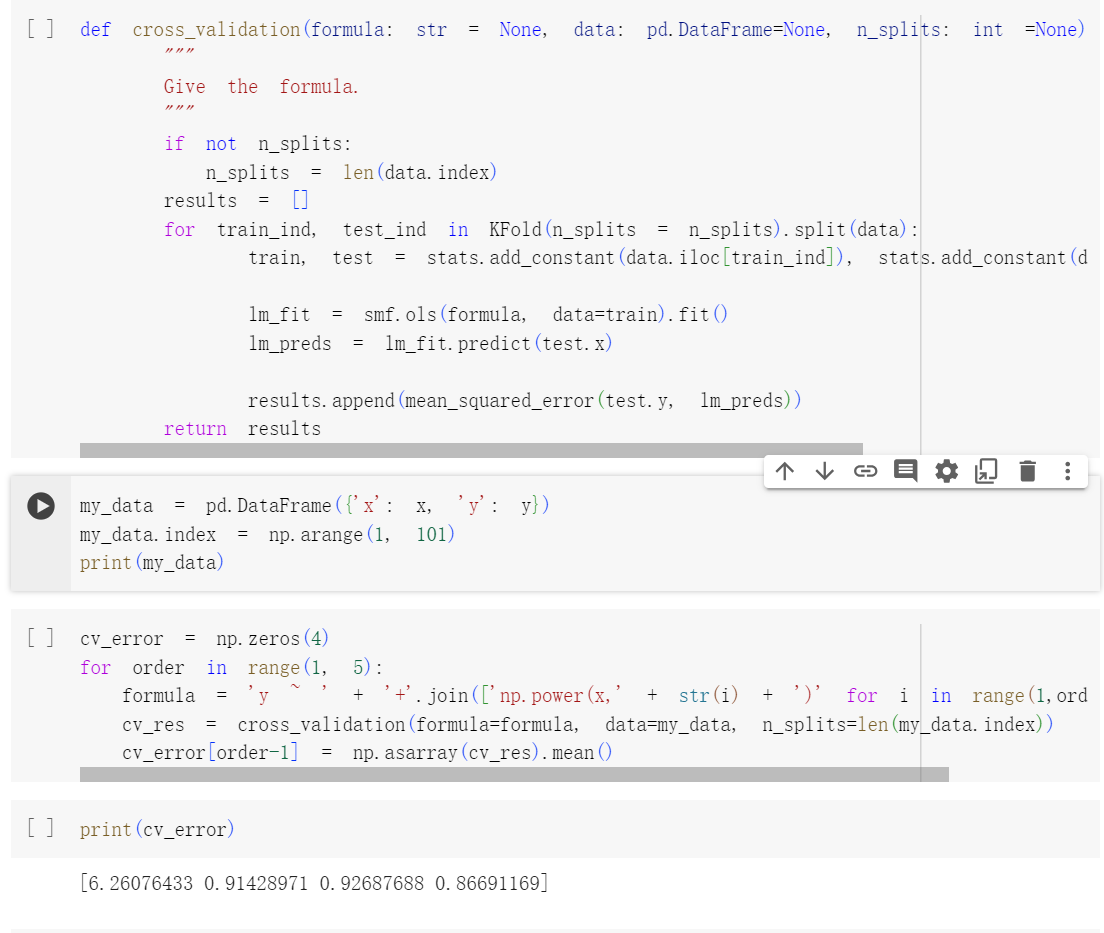
3. 使用最小二乘法拟合以上的每个模型所产生的系数估计值的统计显着性。这些结果与基于交叉验证结果得出的结论一致吗？ 得出的结论X1和X2的t统计值的绝对值是最大的， 所以对应了二次项

   9.

4. 直接计算数据集的std 和mean
5. 通过Bootstrap来估计数据集的std 和mean def boot(var, n): m = np.zeros(n) for i in range(0, n): v    = var.sample(frac=1, replace=True) 就是百分之百，采样，有放回 m[i] = np.mean(v) res1 = np.mean(m) res2 = np.std(m) print('mu: %.5f; se: %.5f' %(res1, res2)) return(res1, res2) 调用： result = boot(medv, 1000) # close to (b)
6. 置信区间
   1. print('lowerbd:%.2f' %(result[0] - 2*result[1])) print('upperbd:%.2f' %(result[0] + 2*result[1]))
   2. from scipy import stats stats.t.interval(0.95,               # confidence level  df = len(df)-1, # degrees of freedom  loc = mu_hat,       # sample mean  scale= mu_hat_se)   # sample std dev
7. 中位数
8. 中位数的标准误差
9. rovide an estimate for the tenth percentile of y # 6.9
10. 生成模拟数据集 np.random.randn(1) 是用来生成一个标准正态分布的随机数的。np.random.randn() 函数生成一个随机数，该随机数服从标准正态分布（均值为0，标准差为1） （1）10* 100 个 X， y是一个多项式 (2) 放到一个数据框里
11. 执行这个两种model selection (1)best subset selection lm = OLS(fit_intercept=True) lm_exhaustive = exhaustive_search(lm, X_new_df, y,nvmax=len(X_new_df.columns)) (2)forward and backward lm = OLS(fit_intercept=True) lm_forward = forward_search(lm, X_new_df, y, nvmax=len(X_new_df.columns)) lm = OLS(fit_intercept=True) lm_backward = backward_search(lm, X_new_df, y, nvmin=1)
12. 现在将==套索模型==拟合到模拟数据，再次使用 X,X2,…,X10 作为预测变量。==使用交叉验证来选择 λ 的最佳值==。(这个其实是一整步，它是一起的)创建作为 ==λ 函数的交叉验证误差图==。（连这个是跟之前那一步一起的）报告所得的==系数估计值==，并讨论获得的结果。==(同时要scale 数据)==
    1. scale scaler = StandardScaler() X_new = scaler.fit_transform(X_new) 2. lambdas = 10 ** np.linspace(3,-3,50)生成1000到0.001的50个等间距的值 mean_scores = np.zeros(len(lambdas)) std_scores = np.zeros(len(lambdas)) for i, lambda_ in enumerate(lambdas): 它用于计算模型在交叉验证中的得分（我scoring设置什么它算什么，cv.mean就得到它的mean） cv = cross_val_score(Lasso(lambda_, max_iter=10000),X_new, y, cv=10, scoring='neg_mean_squared_error') mean_scores[i] = cv.mean() std_scores[i] = cv.std() 3.![[d26871bc8cfbf8b45cc98feed382a87.png]]就是yerr是标准差，lecture也提到了，以标准差作为一个间距 找个mean_scroe最小的一点mn，和对应的lambdas就是opt ![[1e233ecedc7b7977808dd41ae0a9776.png]]这个结果就是，coefficient 为0 的变量就不被考虑了 4.现在根据模型 y=β0+β7X7+e 生成响应向量 y ，并执行最佳子集选择和套索。讨论获得的结果。换了一个模型并执行best subset selection and the lasso

lm_exhaustive.plot()从这些图（RSS，AIC,BIC, R^2 , R^2 adjusted）从看出最佳的变量选择数量是多少，并用以下的代码来展现。 print("AIC:", lm_exhaustive.get_model(n=3)) print("BIC:", lm_exhaustive.get_model(n=1)) print("R2_adj:", lm_exhaustive.get_model(n=5))

6.10

我只是简单地生成 X 和系数的正态分布值 - 这当然可以通过更奇特的方式来完成。我选择将 13 个系数设置为非零值

• 分割train 和test np.random.seed(42) mask = np.random.rand(len(X_df)) < 0.9 train = X_df[mask] test = X_df[~mask] print(mask.shape, train.shape, test.shape) X_train = train.drop('y', axis=1) y_train = train['y'] X_test = test.drop('y', axis=1) y_test = test['y'] 或者 X_train, X_test, y_train, y_test = train_test_split(X_df, y, test_size=0.9, random_state=13)
  1. 生成新的数据集，但是常数给它是个矩阵，同时有一些元素赋值为0，加上执行scale
  2. 分割train和test
  3. 对训练集执行最佳子集选择，plot the training /test set MSE associated with the best model of each size.(这个size指的是特征数，就是自变量的个数) ![[5c1e5e26c06f762a38ba0fd0f4827fc.png]] 这个代码里面，.subset是求这个特定的模型对应的特征值有几个，在做Predict的时候，用到X_train和这个subset 就是这个代码y_pred_trn = model.predict(X_train, subset)
  4. 10e For which model size does the test set MSE take on its minimum value? Comment on your results. If it takes on its minimum value for a model containing only an intercept or a model containing all of the features, then play around with the way that you are generating the data in 10a until you come up with a scenario in which the test set MSE is minimized for an intermediate model size. 对于哪个模型大小，测试集 MSE 取最小值？评论你的结果。如果它对于仅包含截距的模型或包含所有特征的模型呈现最小值，则尝试在 10a 中生成数据的方式，直到您提出一个场景，其中测试集 MSE对于中间模型尺寸被最小化。 print("Minimum test set MSE = {} at {} features".format(np.min(tst_errors), np.argmin(tst_errors)+1))
  5. 测试集 MSE 最小化的模型与用于生成数据的真实模型相比如何？对系数值进行评论???
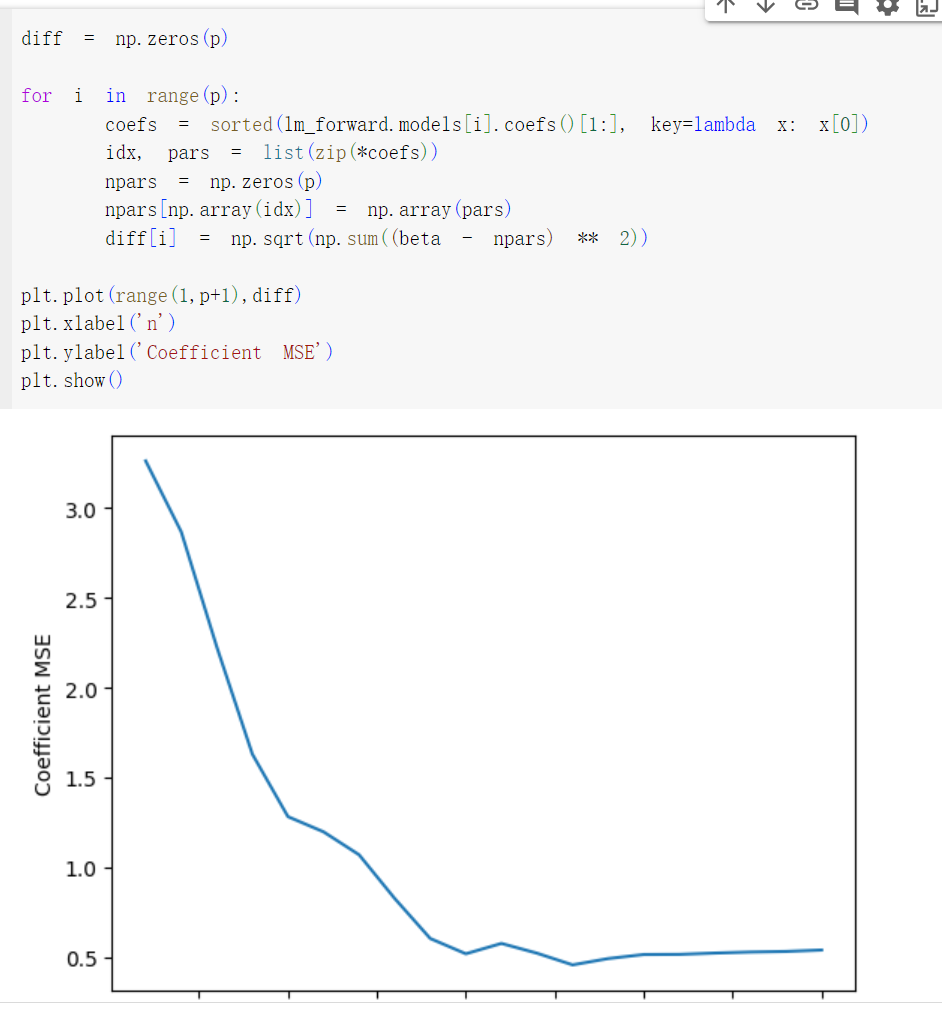
  6. 创建一个图，显示 r 值范围的 ∑pj=1(βj−β^rj)2−−−−−−−−−−−−√ ，其中 βrj 是最佳模型的第 j 系数估计值包含 r 系数。评论你所观察到的事情。这与 的测试 MSE 图相比如何？