W3L1 Unsupervised learning

Lab

PCA

• Scaling
• pca_loadings»>pca_fit.components_.T
• principal component scores»> pca = PCA(random_state=42) pca_df = pd.DataFrame(pca.fit_transform(X_scaled))
• PVE

  Clustering–Hierarchical Clustering

  hc_avg = linkage(X, method='average') hc_complete = linkage(X, method='complete') hc_single = linkage(X, method='single') dend = dendrogram(hc_avg) cut_tree(hc_avg, 2).ravel()就是只聚类了两个类型

• Correlation-based distance can be by passing the method='correlation' argument to the linkage function. 如果我们有一个包含至少三个特征的数据集，我们可以计算两个数据点之间的相关性，并将其视为一种距离度量。具体来说，我们可以使用 Pearson 相关系数来计算相关性。Pearson 相关系数可以度量两个变量之间的线性关系程度

  Applied

  PCA

  1. 获得Proportion Variance Explained(PVE)pca.explained_variance_ratio_
  2. 手动算PVE，不用上面的代码![[a231610ce8f6af47eafbf207cd98180.png]]用这个公式，写这个Loop ![[2421ca477df65ec16149569ec3aaecd.png]]

     hierarchical clustering

  3. 用complete linkage : hc_complete = linkage(USArrests, method ='complete')
  4. 改3个聚类还是4个聚类
  5. 缩放scaling
  6. 画 dendrogram scaler = StandardScaler() X_scaled = scaler.fit_transform(USArrests) hc_complete_sc = linkage(X_scaled, method ='complete') cut_tree(hc_complete_sc, 4).ravel()

dend = dendrogram(hc_complete_sc)

在实际的数据上实践

W3L2 Gaussian Mixture Models

Lab

K-means Clustering

cls = KMeans(n_clusters=2, n_init=20) cls.fit(X) clusters = cls.predict(X) K=2 进行聚类，并进行 20 次初始化(这个初始化就是随机选择选20次)，最后KMeans值报告最佳的值 center = clustering.cluster_centers`得到total within-cluster sum of squares 改变cluster的数量也可以改变簇内平方和

Mixtures-of-Gaussians 

• 这个只适合拟合有高斯分布那种感觉的数据
• 对数似然 ( ll ) 在每次迭代中的变化如何较小，以及最终估计参数如何与我们用于生成数据的参数接近但不相同。
• n_components
• init_params=’kmeans’ （默认值）首先执行 $K$-means 并使用该结果来初始化 EM 算法。一般来说，这会产生更稳定的结果。
• 尝试加入reg_covar = 1e-6会防止过拟合
• covariance_type = ‘diag’/ ‘spherical’考虑到协方差矩阵的分布

  Applied

  PCA and Kmeans

  1. 生成数据集：三个类 各有20个Ob,和50个变量
  2. 对 60 个观测值执行 PCA 并绘制前两个主成分得分向量。 这个分量指的是pca.fit_transform(X)也就是pca_loading的转置
  3. K-means (K=3,2,4)这个结果就是K=3，分的好（看散点图）
  4. 现在执行 K-means在前两个主成分得分向量上而不是在原始数据上使用 K=3 进行聚类: As the clusters are easily separable in 2D, the clusters are exactly equal to the classes and seem less dependent on initialization.
  5. 用StandardScaler()去scaling，但是在这个数据里是没有区别的

     Mixtures of Gaussians

  6. 画个Hist图，看它的数据是不是Gaussian分布
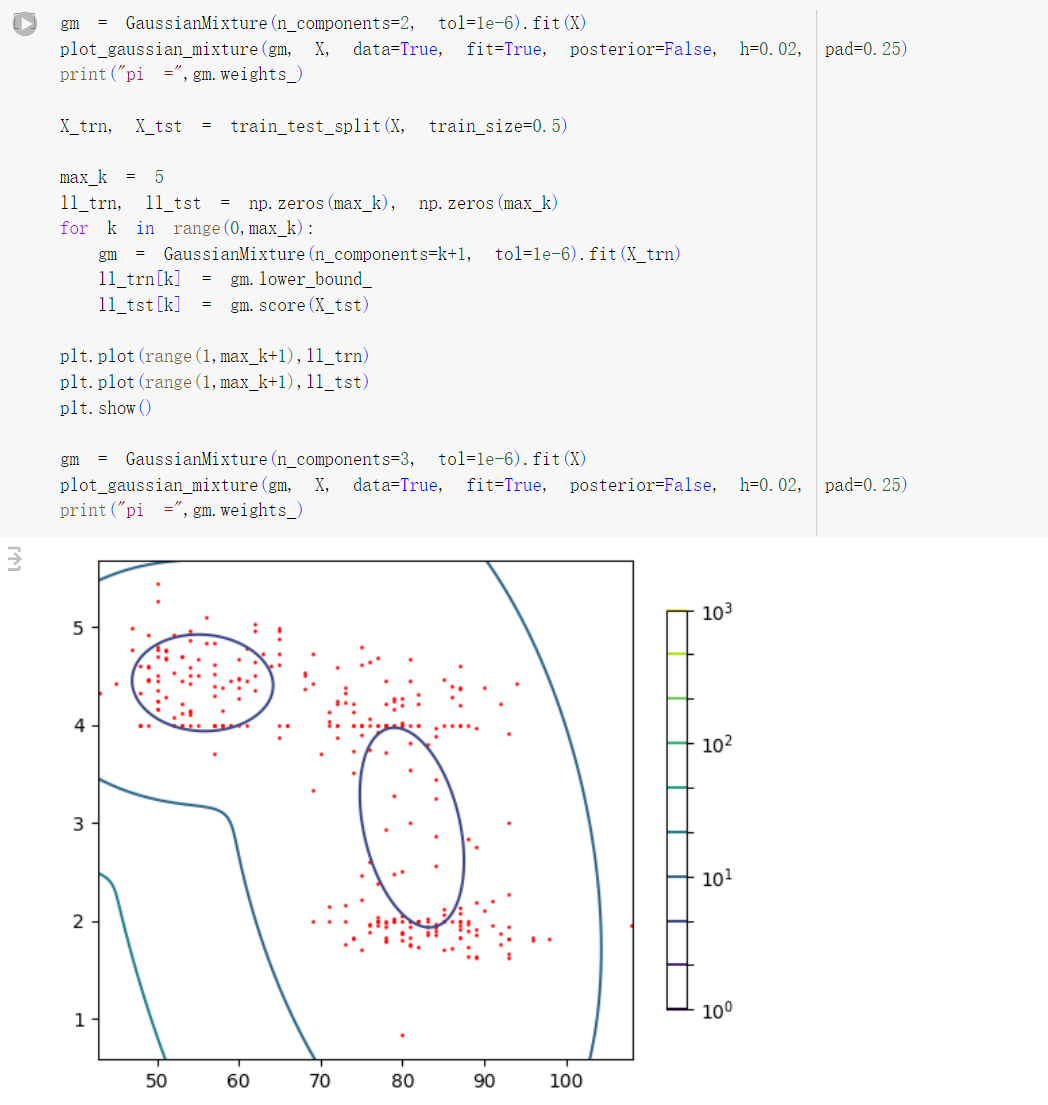
  7. 模型加 mixing proportions: gm = GaussianMiture(n_components=2, verbose=2, verbose_interval=1, tol=1e-6).fit(waiting) print(“pi =”,gm.weights_)` pi = [0.30793897 0.69206103] 哪个分布更有可能生成任意一个数据点。在你的模型中，第一个分布的权重为0.69206103（约为69.2%），第二个分布的权重为0.30793897（约为30.8%）。
  8. 现在用 K=1,2,…5 分量拟合多个高斯混合模型，并将对数似然（拟合模型的属性lower_bound_ ）绘制为 K 的函数»对数似然随着 K 不断增加，因为与训练数据的拟合变得越来越好。然而，从 1 个组件到 2 个组件有明显的跳跃，这表明 2 个组件足以满足该数据
  9. 分了训练集和测试集之后再重复3»实际结果取决于数据的分割，但通常 K>2 的测试集的对数似然会（略微）降低，这表明对于较高的 K 值，模型过度拟合训练数据
  10. Repeat 以上的 steps, but now fitting 2D components to both features at once. What is the optimal number of components?

      W3L3 Deep Learning

      A feed-forward neural network with a single hidden layer

  11. 创建model mlp = Sequential([                 layers.Input(shape=X_train.shape[1]), 输入                   layers.Dense(units=64, activation='relu'), 隐藏层                   layers.Dropout(rate=0.2), 用来validation的一个部分                   layers.Dense(units=1, activation='linear'), 输出层                 ])
  12. mlp.summary()
  13. mlp.compile(loss='mse', metrics=['mae', 'R2Score'], optimizer='rmsprop')
  14. 拟合
  15. 激活函数： ReLU是Rectified Linear Unit的缩写，是一种常用的激活函数，它将输入 x 转换为输出 y 的方法是： Sigmoid函数（也称为Logistic函数）：这是一种经典的激活函数，它将输入映射到一个范围为0到1之间的值。 Tanh函数（双曲正切函数）：这是另一种常用的激活函数，它将输入映射到一个范围为-1到1之间的值。

      解读这两个图

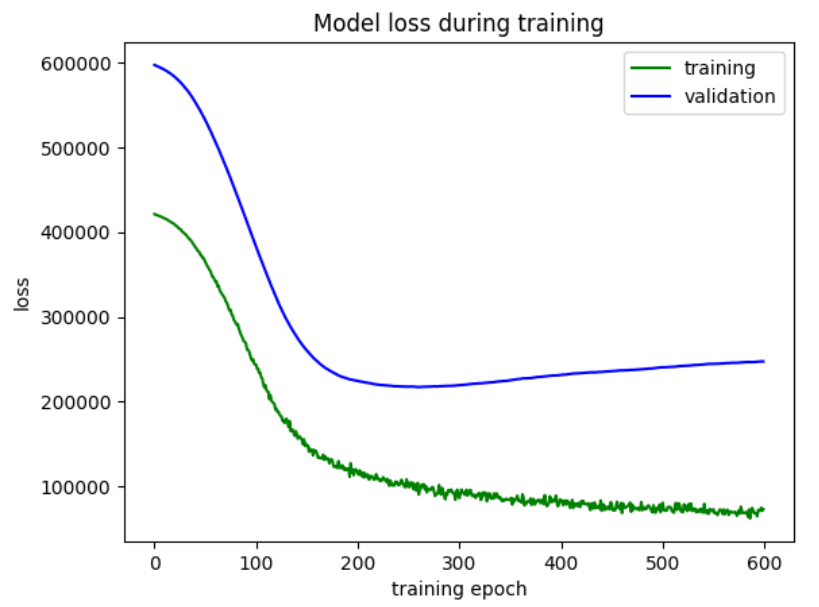
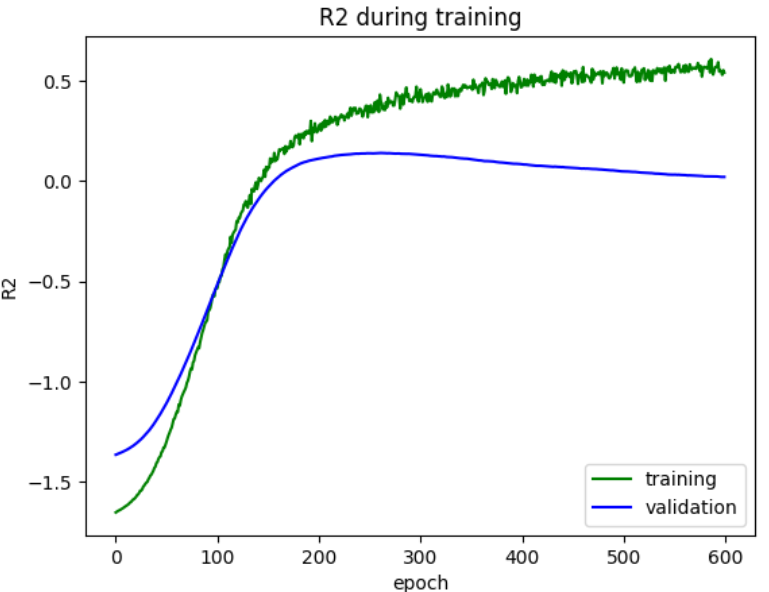      第一个图就是，在拐点的地方(elbow point)，就是150左右，之前是underfiting， 后面validation随着这个epoch的增大而Loss开始增大，就是overfiting。之前validation 都是随着epoch的增大而loss减小。然后training随着一直迭代，loss一直变小。 第二个图就是，在拐点的地方之后validation的R^2开始随着epoch下降，training的R^2开始随着epoch上升，就是过拟合，之前就是underfitting。

      比较Linear, Lasso和MLP

The MNIST dataset with the MNIST dataset

Convolutional Neural Networks with the CIFAR dataset

这个CNN卷积，就是我每卷积一次，它就由一个图变成两个图，最后就是展直了，变成了一个数列一样的只有一列（一维向量）。将特征图展平为一维向量的主要原因之一是为了使得它们可以作为全连接层的输入，提高性能

1. 卷积（Convolution）： 将滤波器与输入图像进行卷积运算，计算出滤波器与图像上每个局部区域的内积。这一步可以理解为提取出图像的局部特征。
2. 激活函数（Activation）： 将卷积后的结果通过激活函数进行非线性变换，从而增加网络的非线性特性。常用的激活函数有 ReLU、sigmoid、tanh 等。
3. 池化（Pooling）： 将卷积后的结果进行池化运算，从而降低特征图的维度，减少参数数量。常用的池化方式有最大池化（Max Pooling）和平均池化（Average Pooling）。