序章
第一部分为数学基础篇,我们会以浅显易懂的方式,铺垫与视觉SLAM相关的数学知识,包括:
•第1讲是前言,介绍这本书的基本信息,习题部分主要包括一些自测题。
•第2讲为SLAM系统概述,介绍一个SLAM系统由哪些模块组成,各模块的具体工作是什么。实践部分介绍编程环境的搭建过程以及IDE的使用。
•第3讲介绍三维空间运动,你将接触到旋转矩阵、四元数、欧拉角的相关知识,并且在Eigen当中使用它们。
•第4讲为李群和李代数。即便你现在不懂李代数为何物,也没有关系。你将学到李代数的定义和使用方式,然后通过Sophus操作它们。
•第5讲介绍针孔相机模型以及图像在计算机中的表达。你将用OpenCV来调取相机的内外参数。
•第6讲介绍非线性优化,包括状态估计理论基础、最小二乘问题、梯度下降方法。你会完成一个使用Ceres和g2o进行曲线拟合的实验。
这些就是我们要用到的所有数学知识了,当然,其中还隐含了你以前学过的高等数学和线性代数。我们保证它们看起来都不会很难。当然,若你想进一步深入挖掘,我们会提供一些参考资料供你阅读,那些材料可能会比正文里讲的知识难一些。
第二部分为SLAM技术篇。我们会使用第一部分所介绍的理论,讲述视觉SLAM中各个模块的工作原理。
•第7讲为特征点法的视觉里程计。该讲内容比较多,包括特征点的提取与匹配、对极几何约束的计算、PnP和ICP等。在实践中,你将用这些方法去估计两个图像之间的运动。
•第8讲为直接法的视觉里程计。你将学习光流和直接法的原理,然后利用g2o实现一个简单的RGB-D直接法。
•第9讲为视觉里程计的实践章,你将搭建一个视觉里程计框架,综合运用先前学过的知识,实现它的基本功能。这个过程中,你会碰到一些问题,例如优化的必要性、关键帧的选择等
第10讲为后端优化,主要为对Bundle Adjustment的深入讨论,包括基本的BA,以及如何利用稀疏性加速求解过程。你将用Ceres和g2o分别书写一个BA程序。
•第11讲主要讲后端优化中的位姿图。位姿图是表达关键帧之间约束的一种更紧凑的形式。你将用g2o和gtsam对一个位姿球进行优化。
•第12讲为回环检测,主要介绍以词袋方法为主的回环检测。你将使用dbow3书写字典训练程序和回环检测程序。
•第13讲为地图构建。我们会讨论如何使用单目进行稠密深度图的估计(以及这是多么不可靠),然后讨论RGB-D的稠密地图构建过程。你会书写极线搜索与块匹配的程序,然后在RGB-D中遇到点云地图和八叉树地图的构建问题。
•第14讲主要介绍当前的开源SLAM项目以及未来的发展方向。相信在阅读了前面的知识之后,你会更容易理解它们的原理,实现自己的新想法
补充
9.*花一个小时学习一下==Vim==,因为你迟早会用它。你可以在终端中输入vimtutor阅读一遍所有内容。我们不需要你非常熟练地操作它,只要能够在学习本书的过程中使用它输入代码即可。不要在它的插件上浪费时间,不要想着把Vim用成IDE,我们只用它做文本编辑的工作。
第一讲 SLAM
SLAM是Simultaneous Localization and Mapping的缩写,中文译作“同时定位与地图构建“
它是指搭载特定传感器的主体,在没有环境先验信息的情况下,于运动过程中建立环境的模型,同时估计自己的运动。
通过人工智能(Arti fi cial Intelligence)和机器学习(Machine Learning)技术,计算机渐渐能够辨 别出物体、人脸、声音、文字——尽管它所用的方式(概率学建模)与我们是如此不同。
在SLAM发展了将近30年之后,我们的相机才渐渐开始能够认识到自身的位置,发觉自己在运动前,与SLAM相关的书籍主要有《概率机器人》(Probabilistic robotics) 、《计算机视觉中的多视图几何》(Multiple View Geometry in Computer Vision)《机器人学中的状态估计》(State Estimation for Robotics:A Matrix-Lie-Group Approach) 数学理论和许多编程知识,会用到==Eigen、OpenCV、PCL、g2o、Ceres==等库
第二讲 初识 SLAM
惯性测量单元(Inertial Measurement Unit,IMU)
它们测到的通常都是一些间接的物理量而不是直接的位置数据。例如,轮式编码器会测到轮子转动的角度,IMU测量运动的角速度和加速度,相机和激光传感器则读取外部环境的某种观测数据。我们只能通过一些间接的手段,从这些数据推算自己的位置。
RGB-D原理
较复杂,除了能够采集到彩色图片之外,还能读出每个像素与相机之间的距离。
单目相机
单目相机拍摄的图像只是三维空间的==二维投影==。我们必须移动相机,才能估计它的运动(Motion),同时估计场景中物体的远近和大小,不妨称之为结构(Structure)。当相机移动时,这些物体在图像上的运动就形成了视差
单目SLAM估计的轨迹和地图将与真实的轨迹和地图相差一个因子,也就是所谓的==尺度(Scale)==
双目相机
双目相机和深度相机的目的,在于通过某种手段==测量物体与我们之间的距离==,克服单目相机无法知道距离的缺点
深度相机(又称RGB-D相机,在本书中主要使用RGB-D这个名称)是2010年左右开始兴起的一种相机,它最大的特点是可以通过==红外结构光或Time-of-Flight(ToF)原理==,像==激光传感器==那样,通过主动向物体发射光并接收返回的光,==测出物体与相机之间的距离==。
经典视觉SLAM框架
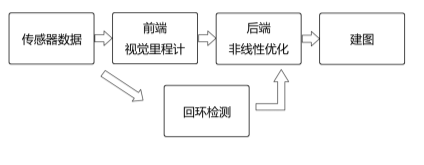
视觉里程计
图像在计算机里只是一个数值矩阵。这个矩阵里表达着什么东西,计算机毫无概念(这也正是现在机器学习要解决的问题)。而在视觉SLAM中,我们只能看到一个个像素,知道它们是某些空间点在相机的成像平面上投影的结果。
相机与空间点的几何关系
VO能够通过相邻帧间的图像估计相机运动,并恢复场景的空间结构。称它为“里程计”是因为它和实际的里程计一样,只计算相邻时刻的运动,而和再往前的过去的信息没有关联。
因为 累积漂移(Accumulating Drift)所以 我们还需要两种技术:后端优化和回环检测
回环检测负责把==“机器人回到原始位置”==的事情检测出来,而后端优化则根据该信息,==校正整个轨迹的形状==。
后端优化
后端优化要考虑的问题,就是如何从这些带有噪声的数据中估计整个系统的状态,以及这个状态估计的不确定性有多大——这称为==最大后验概率估计(Maximum-a-Posteriori,MAP==)。 SLAM问题的==本质==:对运动主体自身和周围环境空间不确定性的估计
回环检测
回环检测与“定位”和“建图”二者都有密切的关系。事实上,我们认为,地图存在的主要意义是让机器人知晓自己到过的地方。为了实现回环检测,我们需要让机器人具有==识别到过的场景的能力==。
建图
度量地图(Metric Map)
稀疏地图进行了一定程度的抽象,并不需要表达所有的物体。例如,我们选择一部分具有代表意义的东西,称之为==路标(Landmark==),那么一张稀疏地图就是由路标组成的地图,而不是路标的部分就可以忽略掉。相对地,稠密地图着重于建模所有看到的东西。对于定位来说,稀疏路标地图就足够了。而用于导航时,则往往需要稠密的地图
对于二维度量地图是许多个小格子(Grid),而对于三维度量地图则是许多小方块(Voxel)。
拓扑地图(Topological Map)
拓扑地图是一个图(Graph),由节点和边组成,只考虑节点间的==连通性==,例如A、B点是连通的,而不考虑如何从A点到达B点。
SLAM问题的数学表述
我们知道三维空间的运动由3个轴构成,所以小萝卜的运动要由3个轴上的平移,以及绕着3个轴的旋转来描述,一共有6个自由度。
PS
这里有一些Linux 和 cmake
第3讲 三维空间刚体运动
主要目标
1.理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。 2.掌握Eigen库的矩阵、几何模块使用方法
旋转矩阵
点和向量和坐标系
坐标系间的欧氏变换
相机视野中某个向量p ,它的坐标为pc,而在世界坐标系下看,它的坐标pw。这两个坐标之间是如何转换的呢?
欧氏变换
相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换
变换矩阵与齐次坐标
我们在一个三维向量的末尾添加1,将其变成了四维向量,称为齐次坐标 
旋转向量和欧拉角 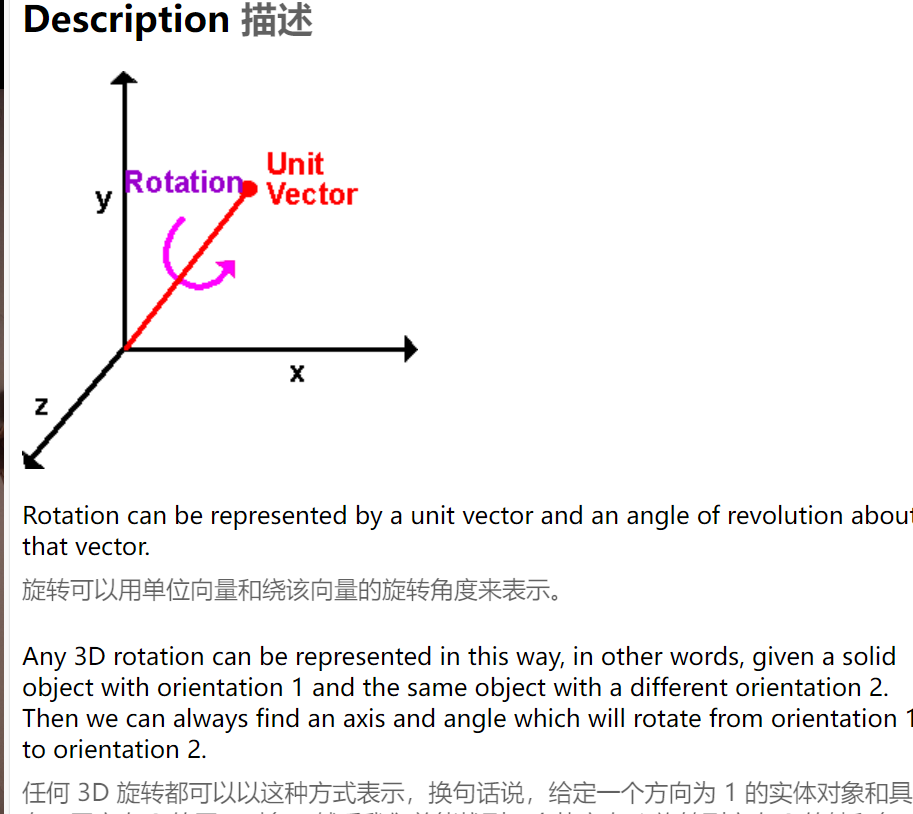 旋转向量和旋转矩阵之间是如何转换的呢? Rodrigues’s Formula
旋转向量和旋转矩阵之间是如何转换的呢? Rodrigues’s Formula
欧拉角 欧拉角则提供了一种非常直观的方式来描述旋转——它使用了3个分离的转角 ,把一个旋转分解成3次绕不同轴的旋转。 你或许在航空、航模中听说过“俯仰角”“偏航角”这些词。欧拉角当中比较常用的一种,便是用“偏航-俯仰-滚转”(yaw-pitch-roll)3个角度来描述一个旋转的。由于它等价于ZY X 轴的旋转 1.绕物体的Z 轴旋转,得到偏航角yaw; 2.绕旋转之后 的Y 轴旋转,得到俯仰角pitch; 3.绕旋转之后 的X轴旋转,得到滚转角roll。
这被称为奇异性问题 万向锁问题(Gimbal Lock[4] ):在俯仰角为± 90° 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由3次旋转变成了2次旋转)。 由于这种原理,欧拉角不适于插值和迭代,往往只用于人机交互中。我们也很少在SLAM程序中直接使用欧拉角表达姿态,同样不会在滤波或优化中使用欧拉角表达旋转(因为它具有奇异性)。不过,若你想验证自己的算法是否有错,转换成欧拉角能够快速分辨结果是否正确。
四元数 我们用复数集C表示复平面上的向量,而复数的乘法则表示复平面上的旋转:例如,乘上复数i 相当于逆时针把一个复向量旋转90° 在表达三维空间旋转时,也有一种类似于复数的代数:四元数 (Quaternion) 
四元数的运算  四元数到旋转矩阵的转换
四元数到旋转矩阵的转换
文档信息
- 本文作者:Xinyi He
- 本文链接:https://buliangzhang24.github.io/2024/12/10/BookNotes-SLAM-Book(Chinese)/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)
